Überprüfbarkeit - Fehlerquellen - Transparenz:

Von der Entwicklung eines Algorithmus bis zu seiner Anwendung und den Handlungen, die auf seinen Ergebnissen basieren, sind oftmals eine große Menge verschiedener Subjekte beteiligt (s. Abbildung 1): Die meisten Algorithmen werden von Wissenschaftlern entwickelt, entweder im akademischen Bereich, im öffentlichen Dienst oder in Firmen. Dies sind entweder Wissenschaftler, die aus einem bestimmten Fachgebiet kommen und für die ihnen vorliegenden Daten neue Analysemethoden entwickeln, z.B. BioinformatikerInnen, oder es sind MathematikerInnen und InformatikerInnen, die ganz allgemein mathematische Probleme mit Hilfe von Algorithmen lösen.

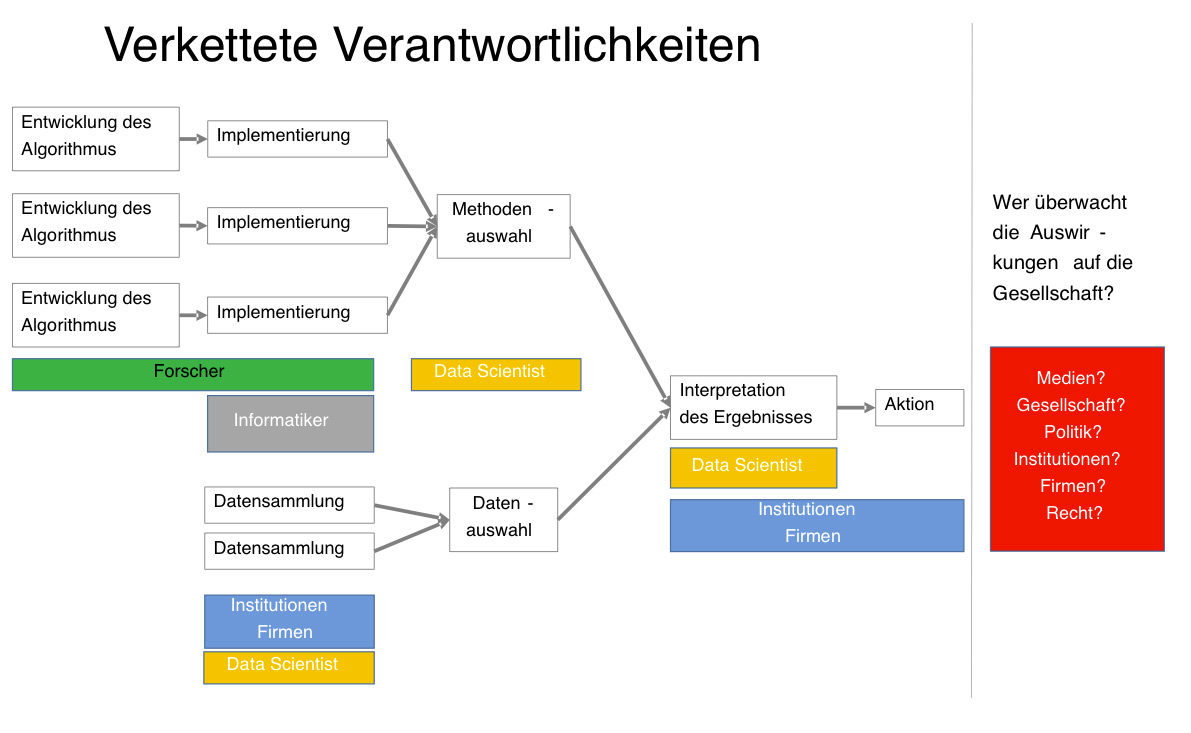
Abbildung 1: Wissenschaftler entwickeln Algorithmen für ein abstraktes, mathematisches Problem. Wenn ein Algorithmus entwickelt wurde, wird er dann implementiert und von einem Data Scientist mit Daten zusammengebracht, um diese interpretieren zu können. Basierend auf der Interpretation werden Handlungen initiiert. Beteiligt an dieser langen Kette von Verantwortlichkeiten sind also Wissenschaftler verschiedener Fachdisziplinen, Informatiker, Datenanalysten und verschiedene Institutionen und Firmen. Wer ist nachher für die Bewertung der gesellschaftlichen Folgen verantwortlich? Ist es die Gesellschaft als Ganzes? Sind es Journalisten oder Politiker oder die Gerichte? Sollte es dafür eine Institution wie den von Viktor Meyer-Schöneberger geforderten Algorithmen-TÜV geben oder sind die einzelnen Firmen selbst dafür verantwortlich?

Oftmals wird erst im Nachhinein klar, dass diese allgemeinen mathematischen Probleme auf vielerlei Fragestellungen angewandt werden können - davor werden sie manchmal nur ganz abstrakt behandelt und gelöst. Entlang dieser langen Kette von Verantwortlichkeiten können nun fünf Arten von Fehlermöglichkeiten identifiziert werden:

1. Konzeptionelle Fehler im Algorithmendesign: In jedem Fall kann es hier zu einem Fehler kommen, indem behauptet wird, dass der Algorithmus ein bestimmtes mathematisches Problem löst, dieses aber nicht der Fall ist. Hier können mehrere Unterfälle auftreten, z.B. dass der Algorithmus gar keinen Fall des Problems korrekt löst, oder eben nur einen Teil davon. Diese Fehler werden bei veröffentlichten Algorithmen von einigem Interesse häufig gefunden. Bei proprietären Algorithmen ist es wahrscheinlich, dass falsche Werte irgendwann auffallen, wenn sie genügend häufig auftreten und genügend stark vom erwarteten Wert abhängen und die Werte nicht direkt in den nächsten Algorithmus eingefüttert werden.

2. Implementierungsfehler: Wenn ein Algorithmus als korrekt gilt, wird in vielen Fällen dann eine erste Implementierung von den beteiligten Wissenschaftlern vorgenommen ("proof of concept"); die dauerhafte Einbindung einer Methode in ein bekanntes Softwarepackage erfolgt  eher durch Gruppen von versierten Programmierern und Programmiererinnen.Dabei kann es zu Programmierfehlern kommen, die den eigentlich korrekten Algorithmus falsch umsetzen und dabei für alle oder manche Fälle des mathematischen Problems falsche Resultate berechnen.

3. Modellierungsfehler: Algorithmen können erst dann gesellschaftlich unerwünschte Nebenwirkungen haben, wenn sie auf die Lösung eines Problems angesetzt werden, das Daten über menschliches Handeln beinhaltet oder Aussagen über (wahrscheinliches) menschliches Handeln machen soll, oder wenn basierend auf der Lösung des Problems Entscheidungen über Menschen und Tiere automatisiert getroffen werden. An dieser Stelle kommt es zu einer Modellierung des Problems, die es erst erlaubt, die eigentliche Frage in Form eines mathematischen Problems von einem dafür geeigneten Algorithmus lösen zu lassen. Ein Beispiel dafür ist die Frage, welche Nachricht aus einem Freundeskreis für eine Person, nennen wir sie Maria, gerade "relevant" ist. Die gewünschte Lösung ist eine Sortierung aller möglichen, neuen Nachrichten für diese Person, die eben dieser "Relevanz" folgt, dafür muss jeder Nachricht eine Zahl zugeordnet werden, so dass eine höhere Zahl mit einer höheren Relevanz gleichzusetzen ist. Es gibt nun Hunderte von Möglichkeiten, diese Relevanz zu quantifizieren, hier davon nur eine kleine Auswahl:

1. Anhand der Länge des Textes;
2. Anhand der bisher beobachteten Wahrscheinlichkeit, dass Maria eine Nachricht von dem Verfasser anklickt;
3. Anhand der bisher beobachteten Wahrscheinlichkeit, dass Maria Nachrichten, die die wichtigsten Wörter dieser Nachricht ebenfalls beinhaltet haben, anklickt;
4. Anhand der bisher beobachteten Wahrscheinlichkeit, dass andere Nutzer diese Nachricht angeklickt haben;
5. Anhand der Zeit, die seit dem Posten der Nachricht vergangen ist.

Natürlich können auch mehrere dieser Ideen miteinander in einer Formel verquickt werden, solange immer noch für jede Nachricht genau eine Zahl berechnet werden kann. David Zuckerberg wird von David Kirkpatrick mit dem Satz zitiert: "A squirrel dying in front of your house may be MORE RELEVANT TO YOUR INTERESTS right now than people dying in Africa." ("the facebook EFFECT", Simon  & Schuster New York, New York, USA, 2010, S. 181). Hier ist also offensichtlich Raum für subjektive Präferenzen, das gilt ganz generell auch für andere Beschreibungen von Fragestellungen als mathematisches Problem.

4. Fehlerhafte oder unzureichende Daten: Algorithmen benötigen immer Eingabedaten. Diese kommen aus den unterschiedlichsten Quellen; dementsprechend variiert auch ihre Qualität. Im Falle von Big Data geht es ganz offen um die Frage, wie man algorithmisch mit Daten umgehen kann, deren Volumen (englisch "Volume") immens ist, deren Wahrheitsgehalt ("Veracity") unklar ist, deren Vielfältigkeit ("Variety") hoch und nicht immer miteinander kompatibel ist, und für die das Resultat unter Umständen so schnell ("Velocity") berechnet werden muss, dass nicht alle Daten in der nötigen Detailtiefe untersucht werden können. Ein offensichtlicher Fehler bezüglich der Daten, auf denen ein Resultat berechnet wird, besteht also darin, dass diese zu fehlerhaft sind um verwendet zu werden.

Fehlerhafte oder unzureichen Daten zu verwenden ist ein qualitativ anderer Fehler als ein Modellierungsfehler: wenn man beispielsweise auf Basis von Daten, die für jeden Kredit, den jemand jemals gehabt hat, nur Zugriff auf die binäre Information hat, ob entweder alle Raten pünktlich bezahlt wurden oder nicht, dann ist es prinzipiell möglich, darauf basierend eine Kreditwürdigkeit zu berechnen.  Um sinnvoll und fair zu sein, sollten aber die Höhe des Kredites, der Zeitpunkt der Kreditnahme und die Höhe der verbliebenen Restschuld, der Grund für eine verspätete Zahlung und die Anzahl der verspäteten Zahlungen berücksichtigt werden. Die erstgenannten Daten wären also inhaltlich unzureichend, für beide Fälle könnte aber derselbe Algorithmus benutzt werden.

Insbesondere bei lernenden Algorithmen können die Daten zum Training des Algorithmus unzureichend sein, indem nicht genügend Datenpunkte für alle zu unterscheidenden Klassen vorhanden sind. Hier erlangten Bilderkennungsalgorithmen von Google und flickr traurige Berühmtheit, weil sie Menschen mit dunkler Hautfarbe nicht korrekt identifizierten. Das liegt meistens daran, dass die Algorithmen an dieser Stelle nicht genügend trainiert werden. Diese nicht ausreichende Datenbasis um Regeln zu lernen ist übrigens auch aus der analogen Welt bekannt: viele psychologische und medizinische Studien werden an "white, educated" persons (mostly males) from "industrialized, rich, democratic countries" durchgeführt ("WEIRD science"). Deren Resultate sind dementsprechend nicht unbedingt auf Frauen und Menschen anderer Kulturen direkt anwendbar.

5. Emergente Phänomene im Zusammenspiel von Algorithmus und Gesellschaft: Ganz zuletzt kann im Wesentlichen alles richtig gemacht worden sein: der Algorithmus löst alle Fälle des mathematischen Problems, die Implementierung ist korrekt, die Modellierung der zu lösenden Frage ist bestmöglich, die Daten sind passend, aber in Zusammenwirkung mit dem Menschen produziert der Algorithmus ungewünschte Ergebnisse. Ein Beispiel dafür ist Googles Suchvervollständigung: Google bietet beim Eintippen von Suchbegriffen Vervollständigungen an. Diese dienen zum Beispiel dazu, einen Rechtschreibfehler zu korrigieren oder dem Nutzer oder der Nutzerin Arbeit zu sparen, indem Varianten, die in letzter Zeit häufig gesucht wurden, angeboten werden. Der Algorithmus nimmt dabei an, dass etwas, was viele Leute in letzter Zeit oft gesucht haben, als voneinander unabhängige Bestätigungen der Wichtigkeit des Themas gelten. Während diese Suchvervollständigung besonders bei technischen Fragen sehr hilfreich sein kann, führen sozial pikante Suchvervollständigungen dazu, dass Menschen, die eigentlich etwas Anderes suchen wollten, sich verleiten lassen, die angebotene Variante anzuklicken. Dadurch kommt es zu einem positiven Feedback, das den Algorithmus veranlasst, diese Alternative mehr Personen bzw. weiter oben anzubieten. Abbildung 2 zeigt die relative Suchhäufigkeit für die Suche nach "Merkel schwanger" bei Google Trends. Man sieht zwei große Maxima.

Abbildung 2: Google Trends zur Suche "Merkel schwanger”, abgefragt am 24.4.2016. Angezeigt wird die relative Suchhäufigkeit dieser Suche - absolute Zahlen sind nicht bekannt.

Das erste wurde vermutlich durch einen Aprilscherz des Radiosenders FFH am 1.4.2009 erzeugt. Das zweite wurde vermutlich durch die Veröffentlichung von Jan Böhmermanns Lied und Video "Mit wem war Mutti im Bett" im Rahmen der Sendung "NEO MAGAZIN ROYALE" (Veröffentlichung auf YouTube am 7.5.2015) erzeugt. Es ist zu vermuten, dass die ersten Anfragen sich auf die jeweiligen Sendungen bezogen, dass dann aber weitere Suchende, die eigentlich nicht über Merkels Schwangerschaft aufgeklärt werden wollten, über die Suchvervollständigung auf diesen vermeintlichen Fakt aufmerksam wurden und dann ebenfalls darauf klickten. Eine ähnliche Dynamik gab es vermutlich auch bei dem Fall von Bettina Wulff. Abbildung 3 zeigt die relative Suchhäufigkeit für "Wulff Rotlicht". Interessanterweise erkennt Googles Algorithmus eine Verwandtschaft mit der Suche nach "Christina Wulff Rotlicht", vermutlich anfangs eine Suche mit Tippfehler, da die beteiligten Personen Bettina und Christian Wulff sind, wobei die erste Ehefrau von Wulff Christiane Wulff hieß (Abbildung 4).

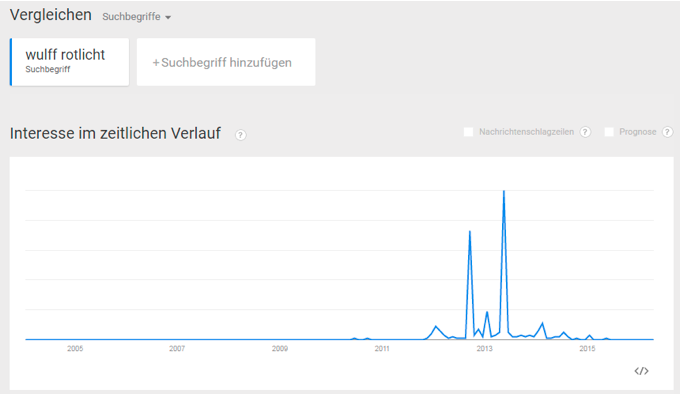
Abbildung 3: Relative Suchhäufigkeit für "Wulff Rotlicht”.

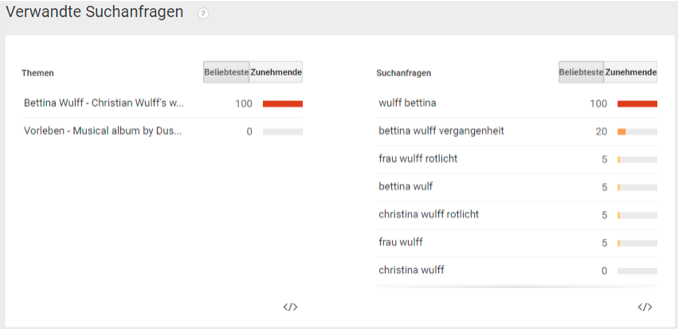
Abbildung 4: Auch die Anfrage "Christina Wulff rotlicht” hat einige Aufmerksamkeit auf sich gezogen. Hier scheint es sich um einen Tippfehler zu handeln, eine Mischung aus "Christian Wulff” und "Christiane Wulff” (1. Ehefrau).

Zusammenfassung  möglicher Fehlerquellen

Es gibt also fünf Klassen von Fehlerquellen:

1. Fehlerhafte Algorithmen, also Problemlösestrategieren für ein gegebenes mathematisches Problem, die das Problem nicht vollständig korrekt lösen.
2. Fehlerhafte Implementierung eines für sich genommen korrekten Algorithmus.
3. Fehlerhafte Modellierung von der zu beantwortenden Frage auf ein passendes mathematisches Problem.
4. Zu fehlerbehaftete Daten oder sonstwie unpassende Daten. Dies umfasst die Frage, ob die Datengrundlage für die Beantwortung der gestellten Frage geeignet ist, insbesondere bei lernenden Algorithmen.
5. Gesellschaftlich unerwünschte Nebenwirkungen aufgrund der Interaktion eines eigentlich korrekten Algorithmus inklusive einer sinnhaften Modellierung mit menschlichem Verhalten.

Minimale Forderungen an die Transparenz von Algorithmen, um Überprüfbarkeit zu ermöglichen

Bei der Frage nach der Überprüfbarkeit eines Algorithmus geht es um die Teilklasse von Algorithmen, die überhaupt gesellschaftliche Auswirkungen oder Nebenwirkungen erwarten lassen. Diese müssen bezüglich der oben genannten Fehlerquellen untersuchbar sein.

Dazu ist es also zuallererst notwendig, das mathematische Problem zu kennen, das durch den Algorithmus gelöst werden soll. Nur damit können der grundlegende Algorithmus und seine Implementierung ganz prinzipiell auf Korrektheit untersucht werden. Dies schließt die Frage ein, auf welcher abstrakten Datengrundlage der Algorithmus arbeitet. Es ist allerdings wichtig zu beachten, dass es für eine klärende Instanz notwendig sein kann, auch direkten Zugang zum Code zu bekommen, um die Korrektheit prüfen zu können.

Die Modellierung und ihre vereinfachenden Annahmen müssen transparent gemacht werden. Dazu ist es notwendig, die zu beantwortende Frage genau zu formulieren und wie diese mit dem mathematischen Problem, das der Algorithmus löst, zusammenhängt. Insbesondere sind die subjektiven Entscheidungen und Vereinfachungen zu benennen, die zwangsläufig bei einer Übersetzung einer Frage in ein mathematisches Problem auftauchen.

Danach ist die Kenntnis und Untersuchung der realen Datengrundlage wichtig, zusammen mit Kennzahlen über die Fehlerrate der einzelnen Datenbestandteile.

Aufgrund der sich häufig ändernden Algorithmen großer Konzerne ist es zudem notwendig, eine Forensik betreiben zu können, so dass beispielsweise Fälle mutmaßlicher Diskriminierung mit zeitnah erhobenen Daten untersucht werden können.

Bei alldem ist es notwendig, dass Forderungen nach Transparenz zielführend und den möglichen Auswirkungen und Nebenwirkungen auf die Gesellschaft angemessen sind. Eine vollständige Offenlegung des Codes gegenüber der Öffentlichkeit ist, beispielsweise, nicht zielführend, da der Code alleine in den wenigsten Fällen selbsterklärend ist. Es ist auch nicht angemessen, da beispielsweise bei Produktempfehlungsalgorithmen die volle Kenntnis des Algorithmus seitens der Produzenten dazu führen könnten, dass ein eigentlich sinnvoller Algorithmus durch Manipulationen ausgehebelt wird.

Viktor Mayer-Schöneberger fordert daher den Berufsstand des "Algorithmikers", der ähnlich einem Betriebsprüfer, Einblick in Algorithmen bekommt und deren Korrektheit nach außen bestätigt.

Begriffserklärung 

Algorithmus: Ein Algorithmus löst ein mathematisches Problem, d.h., er beschreibt einen für den Computer korrekt interpretierbaren Lösungsweg, der für jede durch das mathematische Problem definierte mögliche Eingabe die korrekte Lösung in endlicher Zeit berechnet. Warum in endlicher Zeit? Weil Lösungswege denkbar sind, bei denen man unendlich lange auf die Lösung warten muss. Dazu gehört der folgende Sortieralgorithmus: Bringe die Dinge in eine zufällige Reihenfolge und prüfe für jedes Paar von Dingen, die in der Reihenfolge direkt nebeneinander stehen, ob diese richtig herum stehen. Wenn dies der Fall ist, gib die Reihenfolge aus - diese ist sortiert. Da aber jedes Mal eine zufällige Reihenfolge gewählt wird, gibt es keine Garantie, dass jemals eine korrekte  Lösung ausgegeben wird. Hier handelt es sich nicht um einen Algorithmus. Auch die berühmte Analogie zu einem Kochrezept funktioniert in den allermeisten Fällen nicht, da viele Begriffe benutzt werden, die in dieser Form nicht direkt von einem Computer interpretiert werden können, z.B. "Nudeln bissfest kochen" oder "eine Prise Salz zugeben". Diese Angaben müssten in eine Form gebracht werden, die für den Kochroboter sensorisch erfasst werden können (z.B. benötigter Druck um Nudel zu zerteilen) oder in genaue Mengen ("1 g Salz") übersetzt werden.

Algorithmische Entscheidungsfindung (algorithmic decision making, ADM) setzt sich aus den folgenden Bestandteilen zusammen:

1. Prozesse zur Datenerfassung zu entwickeln,
2. Daten zu erfassen,
3. Algorithmen zur Datenanalyse zu entwickeln, die
   1. die Daten analysieren,
   2. auf der Basis eines menschengmachten Deutungsmodells  interpretieren,
   3. und automatisch handeln, indem die Handlung mittels eines menschengemachten Entscheidungsmodells aus dieser Interpretation abgeleitet wird.

Data Mining: Als Data Mining bezeichnet man die Suche nach Mustern in meist großen Datenmengen. Oftmals wird das Muster selbst vorgegeben, z.B. wird nach zwei Ereignissen gesucht, die häufig miteinander auftreten. Ein berühmtes Beispiel ist die Entdeckung von Target, dass Schwangere oft Produkte kaufen, die in ihrer Häufung so ungewöhnlich sind, dass sie dadurch zu einem gewissen Prozentsatz identifizierbar sind.

Heuristik: Eine Heuristik versucht eine Lösung für ein Optimierungsproblem zu finden, ohne zu garantieren, dass es die optimale Lösung ist. Heuristiken werden dann verwendet, wenn es zwar grundsätzlich möglich ist, die optimale Lösung zu finden, dies aber zu lange dauern wird. Wir Menschen benutzen beispielsweise eine Heuristik, um die kürzeste Route von A nach B auf einer Landkarte zu verwenden: wir suchen nach dem augenscheinlich kürzesten Weg auf eine Autobahn, dann nach dem augenscheinlich kürzesten Weg über die Autobahnen in die Nähe von B und dann nach dem augenscheinlich kürzesten Weg von der Autobahn zum Zielort. Das Verfahren garantiert keine kürzeste Route (weder in der Gesamtdistanz noch Gesamtfahrzeit), ist aber meistens auch nicht allzu weit davon entfernt.

Implementierung: Die Implementierung eines Algorithmus beschreibt die Übersetzung der Handlungsanweisungen in eine konkrete Programmiersprache, so dass der Computer nach Ausführen des dabei entstehenden Codes das zugehörige mathematische Problem für jede Eingabe lösen kann.

Lernender Algorithmus: Bei "lernenden" Algorithmen besteht die eigentliche Berechnung eines Resultates aus zwei verschiedenen Phasen: in der ersten Phase versucht der Algorithmus Regeln in Daten zu lernen, die auf die gewünschte Entscheidung hindeuten. Dies geschieht oft "unter Aufsicht", d.h., dem Algorithmus wird bezüglich historischer Daten mitgeteilt, ob diese ein gewünschtes Ergebnis hatten oder nicht. Beispiel könnte wieder die Kreditwürdigkeit sein, wo ein Algorithmus basierend auf vielen verschiedenen Daten und der Information, ob ein Kredit vollständig zurückgezahlt wurde oder nicht, Regeln dafür sucht, welche Informationen am ehesten auf eine hohe Wahrscheinlichkeit für die Rückzahlung eines zukünftigen Kredits hindeuten. In der zweiten Phase werden diese Regeln dann benutzt, um Entscheidungen aufgrund derselben Art von Daten zu treffen, ohne das wirkliche Ergebnis zu kennen.

Mathematisches Problem: Ein mathematisches "Problem" definiert, welches gewünschte Resultat basierend auf den eingegebenen Daten berechnet werden soll. Dazu gibt das Problem auch an, für welche Art von Eingabedaten das zuverlässig berechnet werden können soll. Beispiele: das "Kürzeste-Wege-Problem" oder das "Sortierproblem". Oftmals werden die Eingabe und die gewünschte Ausgabe mit den einleitenden Worten Gegeben und Gesucht beschrieben. Wie man am untenstehenden Sortierproblem sehen kann, ist es möglich, dass verschiedene Ausgaben die gewünschte Eigenschaft haben. Außerdem kann ein und dasselbe Problem durch verschiedene Algorithmen gelöst werden, d.h., es wird genau dieselbe Lösung berechnet, wenn diese eindeutig bestimmt ist. Gibt es mehrere Lösungen, die die Anforderungen erfüllen, kann jeder Algorithmus eine andere davon berechnen.

Modellierung: Während viele mathematische Probleme sich so anhören, als wären sie direkte Abbilder der in der Realität zu beantwortenden Fragen, gibt es immer einen mehr oder weniger großen Modellierungsfreiraum - Beispiele dafür geben wir unter den Schlagworten Kürzeste-Wege-Problem und Sortier-Problem. Andere Fragen bieten deutlich mehr Spielraum bei der Auswahl des mathematischen Problems, das eigentlich zu lösen ist. Ein Beispiel hierfür ist die Frage nach der zentralsten, wichtigsten Person in einer sozialen Struktur, z.B. einer Firma. Hier gibt es Dutzende von Ansätzen, die die Frage zum Beispiel danach beantworten, wieviele Untergebene jemand hat, wie sehr er oder sie die Kommunikation von anderen kontrollieren kann, oder wie zentral und wichtig seine direkten Bekannten sind. Jede dieser Interpretationen der Frage wird durch ein anderes mathematisches Problem repräsentiert.

Optimierungsproblem: Als wichtige Spezialklasse der mathematischen Probleme gibt es die Gruppe der Optimierungsprobleme. Diese bekommen eine Menge von Eingaben und definieren eine Menge von grundsätzlichen Lösungen. Auf dieser Menge definieren sie zusätzlich für jede mögliche Lösung eine Kostenfunktion (oder eine Gewinnfunktion). Gesucht wird dann nach der Lösung mit den geringsten Kosten (oder dem höchsten Gewinn). Das Kürzeste-Wege-Problem kann man als Optimierungsproblem repräsentieren, wenn man grundsätzlich alle Routen von Startpunkt zu Ziel als mögliche Lösungen definiert plus einer Kostenfunktion, die dann entweder der Gesamtlänge oder Gesamtfahrzeit entspricht.

Softwarepackage: in vielen Bereichen im Data Mining und der Datenanalyse gibt es Softwarepakete, die es relativ einfach machen, komplizierte Analysemethoden in Form von Algorithmen auf seine eigenen Daten anzuwenden. Viele dieser Pakete werden von Doktoranden und Doktorandinnen zusammengestellt und frei zugänglich gemacht (wie z.B. in R), andere müssen gekauft werden (wie z.B. Mathematica).

Sortierproblem: Gegeben eine Menge von Dingen und eine Eigenschaft, so dass man für jedes Paar bestimmen kann, ob in einer nach der Eigenschaft sortierten Reihenfolge das eine vor dem anderen kommt oder umgekehrt oder ob beide an derselben Stelle stehen sollte. Beispiel: Gegeben eine Menge von Büchern, die nach dem Nachnamen ihres Erstautoren sortiert werden sollen, kann man für je zwei Bücher bestimmen, welches vor dem anderem einsortiert werden muss. Stammen beide von Autoren mit demselben Nachnamen, dann ist bei dieser Variante egal, welche zuerst einsortiert wird - jede Lösung, die alle anderen Paare korrekt einsortiert ist eine mögliche Ausgabe. Natürlich kann das Sortierproblem so variiert werden, dass bei gleichem Nachnamen noch nach dem Vornamen entschieden wird, und wenn dieser auch gleich ist, nach dem Erstpublikationsjahr unterschieden werden soll.